目录
快速导航-

教学纵横 | 基于核心素养的高中数学探究性作业设计实践
教学纵横 | 基于核心素养的高中数学探究性作业设计实践
-

教学纵横 | 数学教学应强化学生思维品质的培养
教学纵横 | 数学教学应强化学生思维品质的培养
-

教学纵横 | 高中数学大单元视域下的习题课讲评
教学纵横 | 高中数学大单元视域下的习题课讲评
-

教学纵横 | 基于“问题链”设计的习题课题型探究
教学纵横 | 基于“问题链”设计的习题课题型探究
-

教例探微 | 由一道模考题教学谈高效试卷讲评课
教例探微 | 由一道模考题教学谈高效试卷讲评课
-
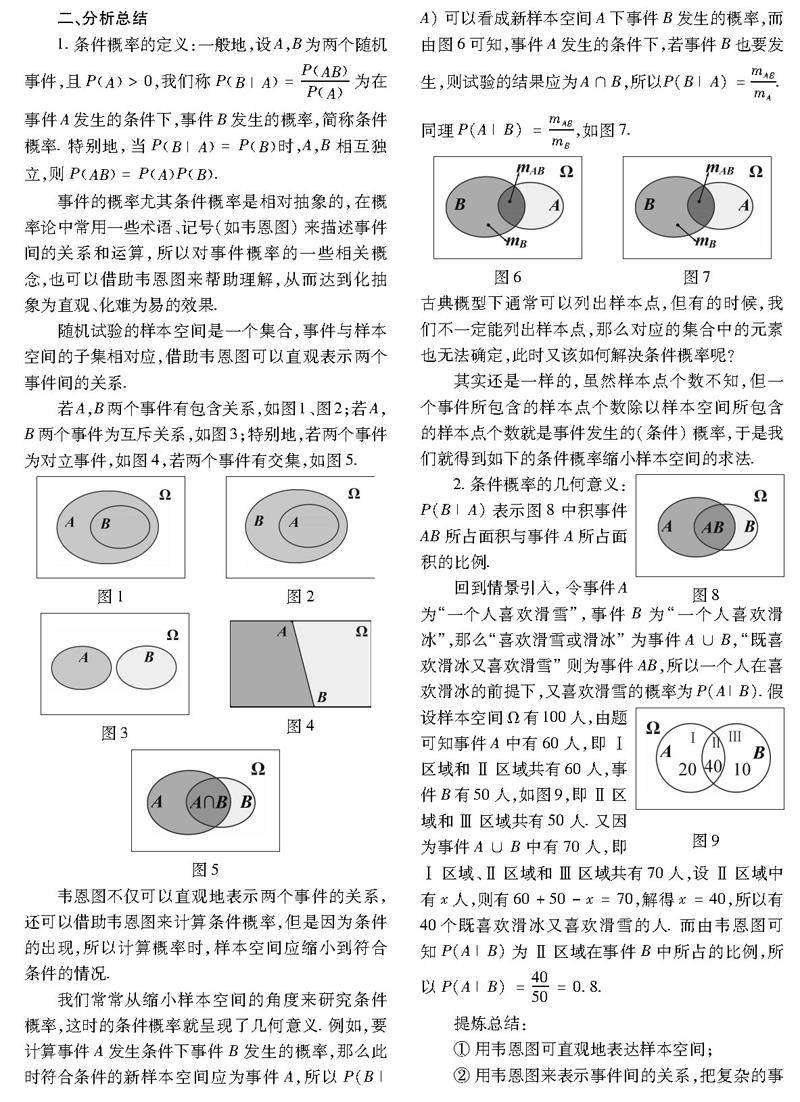
教例探微 | 韦恩图视角下的条件概率
教例探微 | 韦恩图视角下的条件概率
-

教例探微 | 对一道概率模拟试题的变式探究
教例探微 | 对一道概率模拟试题的变式探究
-

聚焦高考 | 对2024年天津高考卷第15题的解法探究
聚焦高考 | 对2024年天津高考卷第15题的解法探究





























 登录
登录