目录
快速导航-

教学纵横 | 基于单元教学设计理念对《复数》教学的思考
教学纵横 | 基于单元教学设计理念对《复数》教学的思考
-

教学纵横 | 高中数学试题情境的设计与实践
教学纵横 | 高中数学试题情境的设计与实践
-

教学纵横 | 统计教学要凸显合理性
教学纵横 | 统计教学要凸显合理性
-

教学纵横 | 寻根究源,优化思路,提升素养
教学纵横 | 寻根究源,优化思路,提升素养
-

教例探微 | 一题多解显素养
教例探微 | 一题多解显素养
-
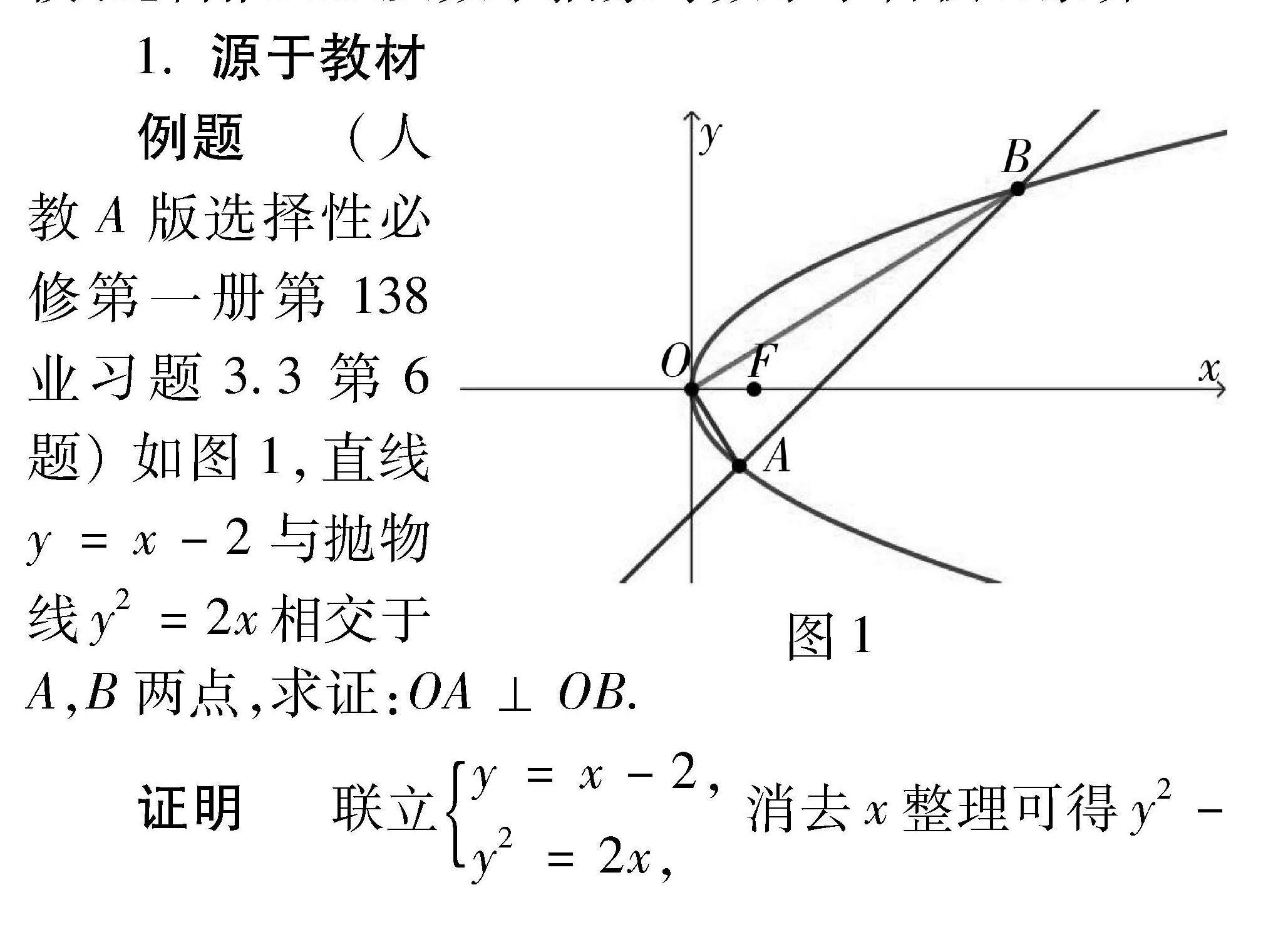
教例探微 | 一题多变:典型教材习题的探究与拓展
教例探微 | 一题多变:典型教材习题的探究与拓展
-

教例探微 | 挖掘问题内涵,巧妙思维应用
教例探微 | 挖掘问题内涵,巧妙思维应用
-

教例探微 | 貌合神离的条件概率与积事件概率
教例探微 | 貌合神离的条件概率与积事件概率

































 登录
登录